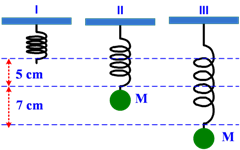
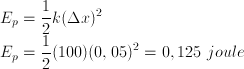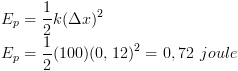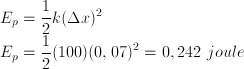Soal dan Pembahasan Elastisitas Part. 2

Soal Dan Pembahasan Elastisitas Part. 2

1. Sebuah keluarga yang terdiri dari empat orang yang total massanya 200kg masuk ke dalam mobil sehingga pegas mobil tertekan ke bawah sejauh 3 cm. Dengan menganggap pegasnya tunggal, berapakah tetapan pegas mobil itu?

a. 6,5 × 10⁴ N/m

b. 7,5 × 10³ N/m

c. 6,5 × 10³ N/m

d. 7,0 × 10⁴ N/m

e. 7,5 × 10⁴ N/m

Pembahasan:

Gaya berat w=m.g

                   = (200 kg)(9,8 m/s²)

                   = 1.960 N (menyebabkan pegas tertekan sejauh x = 3 cm = 0,03 m)

Oleh karena itu,di peroleh :

k = F/ x

= 1960 N/0,03 m

= 6,5 ×10⁴ N/m (a)

2. Sebuah beban bermassa m digantungkan pada ujung bawah pegas dengan tetapan pegas k= 50 N/m. Berapa periode osilasi pegas?

a. 2,8 s

b. 0.26 s

c. 0,28 s

d. 1,25 s

e. 2,5 s

Pembahasan:    

Periode osilasi (T) ditentukan dengan persamaan :

T = 2π √ m/k

   = 2 π√ 0,1 kg/ 50 N/m

   = 0,28 s (c)

3. Panjang tali ayunan adalah 20 cm, jika perceepatan gravitasi 10m/s² dan sudut elevasi 37º. Berapa besar gaya pemulih pada kedudukan tersebut?

a. 2,5 N

b. 2,4 N

c. 2,7 N

d. 3,0 N

e. 3,5 N

Pembahasan:

Besar gaya pemulih dapat dihitung dengan persamaan :

F = m.g sin θ

   = (0,4 kg)(10 m/s²) (sin 37º)

   = (0,4 kg)(10 m/s²)( 0,6 )

   = 2,4 N (b)

4. Seekor nyamuk dengan massa 0,20 gram terperangkap di sarang laba-laba. Jika sarang tersebut bergetar dengan frekuensi 20 Hz, berapa nilai konstanta pegas sarang tersebut?

a. 3,5 N/m

b. 4,0 N/m

c. 3,10 N/m

d. 2,50 N/m

e. 3,15 N/m

Pembahasan:

m = 0,20 gr = 2 × 10^-4

menggunakan persamaan frekuensi, yaitu :

f = 1 √ k/m

     2π

k = (2πf)² × m

k  = (6,28 × 20)²  × 2 × 10^-4

k = 3,15 N/m (e)

5. Dua pegas masing-masing dengan tetapan 2 N/m. Jika disusun secara paralel, maka tetapan pegas susunan adalah

a. 0,25 N/m

b. 3 N/m

c. 1,5 N/m

d. 2,5 N/m

e. 4 N/m

Pembahasan:

pararel = k_{1 +} k₂

k₁ = 2 N/m

k₂ = 2 N/m

k_total  = k₁ + k₂

k_total  = 2 N/m + 2 N/m

        = 4 N/m (e)

6. Diberikan gaya pada suatu pegas 200 N dengan luas penampang batang 50 m². Berapa tegangan yang di hasilkan dari pegas tersebut?

a. 9,0 N/m²

b. 5,0 N/m²

c. 4,0 N/m²

d. 3,0 N/m²

e. 2,5 N/m²

Pembahasan:

tegangan = stress = σ

σ = F /A

F = 200 N

A = 50 m²

σ  = 200 N/ 50 m² = 4,0 N/m² (c)

7. Sebuah kawat luas penampangnya 4 mm² dan panjangnya 10 m. Kawat diregangkan dengan gaya 48 N. Jika modulus young tembaga 12 × 10¹⁰ N/m². Berapa pertambahan panjang kawat?

a. 14 × 10^-4 m

b. 13 × 10^-4 m

c. 12 × 10^-4 m

d. 11 × 10^-4 m

e. 10 × 10^-4 m

Pembahasan:

Δl? disini kita memakai persamaan dari rumus modullus young (E)

E = σ /ε

    = (F/A)/(Δl/l)

    = F.l / A.Δl

Δl =( F.l )/ (E.A)

    = (48 N. 10 m) / (12 × 10¹⁰ × 4× 10^-6)

    = 10 × 10^-4 m (e)

8. Sebuah pegas mula-mula panjangnya 20cm. Kemudian pada salah satu ujungnya digantungkan beban 2 kg, ternyata panjang pegas menjadi 25cm. Jika g = 10 m/s². Berapa konstanta pegas tersebut?

a. 400 N/m

b. 300 N/m

c. 250 N/m

d. 200 N/m

e. 150 N/m

Pembahasan:

F = k.Δx

k = F / Δx

F = m. g = 2 × 10 = 20 N

Δx = 0,25 – 0,20 = 5 × 10^-2 m

k = 20 N/ 5 × 10^-2 m

   = 400 N/m (a)

9. Sebuah bergetar dengan frekuensi 40 Hz selama 1 menit karena di beri gaya 30 N. Berapakah fase getarannya?

a. 240

b. 2400

c. 3600

d. 360

e. 250

Pembahasan:

f = 40 Hz  dan t = 1 menit = 60 s

T = 1/f

   = 1/ 40

fase getaran  = t/ T

                      = 60 / 1/40

                      = 60 . 40 /1

                      = 2400 (b)

10. Sebuah pegas yang diberi beban bergetar harmonis dengan amplitudo 12cm dan periode 0,5 detik. Berapakah kecepatan partikel saat simpangannya 6cm?

a. 13,005 m/s

b. 12,67 m/s

c. 1,305 m/s

d. 1,267 m/s

e. 12,18 m/s

Pembahasan:

Kecepatan jika y = 6 cm

y = A sin (2π.t/T )

6  = 12 sin (360.t/0,5)

Misalkan (360.t/0,5) = x maka :

6      = 12 sin x

sin x = 6/12

sin x = 0,5

x      =  30º

cos (360.t/T) = cos x = cos 30º = ½ √3

maka kecepatannya :

            v = 2πA/T cos (360.t/T)

               =( 2π × 12/0,5) (1/2√3)

               = (12 π/0,5)(√3)

               =  24π √3

               = 130,53 cm/s

               =  1,305 m/s (c)

Soal dan Pembahasan Elastisitas Part.1

Soal dan Pembahasan Elastisitas Part.1

1.

Tentukan :
a) Nilai konstanta pegas
b) Energi potensial pegas pada kondisi II
c) Energi potensial pegas pada kondisi III ( benda M kemudian ditarik sehingga bertambah panjang 7 cm)
d) Energi potensial sistem pegas pada kondisi III
e) Periode getaran yang terjadi jika pegas disimpangkan hingga bergetar harmonis
f) Frekuensi getaran pegas

Pembahasan

a) Nilai konstanta pegas
Gaya-gaya yang bekerja pada benda M saat kondisi II adalah gaya pegas dengan arah ke atas dan gaya berat dengan arah ke bawah. Kedua benda dalam kondisi seimbang. 



b) Energi potensial pegas pada kondisi II



c) Energi potensial pegas pada kondisi III ( benda M kemudian ditarik sehingga bertambah panjang 7 cm)



d) Energi potensial sistem pegas pada kondisi III



e) Periode getaran yang terjadi jika pegas disimpangkan hingga bergetar harmonis



f) Frekuensi getaran pegas



Soal No. 2
Enam buah pegas identik disusun sehingga terbentuk seperti gambar di bawah. Pegas kemudian digantungi beban bermassa M .

Jika konstanta masing-masing pegas adalah 100 N/m, dan massa M adalah 5 kg, tentukan :
a) Nilai konstanta susunan pegas
b) Besar pertambahan pertambahan panjang susunan pegas setelah digantungi massa M

Pembahasan
a) Nilai konstanta susunan pegas

b) Besar pertambahan pertambahan panjang susunan pegas setelah digantungi massa M

Soal No. 3
Perhatikan gambar berikut! Pegas-pegas dalam susunan adalah identik dan masing-masing memiliki konstanta sebesar 200 N/m.
Gambar 3a


Gambar 3b

Tentukan :
a) nilai total konstanta susunan pegas pada gambar 3a
b) nilai total konstanta susunan pegas pada gambar 3b

Pembahasan
a) nilai total konstanta susunan pegas pada gambar 3a
Susunan pada gambar 3a identik dengan 4 pegas yang disusun paralel, sehingga k_tot = 200 + 200 + 200 + 200 = 800 N/m

b) nilai total konstanta susunan pegas pada gambar 3b

Soal No. 4
Sebuah benda bermassa M = 1,90 kg diikat dengan pegas yang ditanam pada sebuah dinding seperti gambar dibawah! Benda M kemudian ditembak dengan peluru bermassa m = 0,10 kg.

Jika peluru tertahan di dalam balok dan balok bergerak ke kiri hingga berhenti sejauh x = 25 cm, tentukan kecepatan peluru dan balok saat mulai bergerak jika nilai konstanta pegas adalah 200 N/m!

Pembahasan
Kecepatan awal gerak balok (dan peluru di dalamnya) :

Soal No. 5
Perhatikan gambar berikut ini!
Tentukan :
a) nilai konsanta pegas
b) energi potensial pegas saat x = 0,02 meter
(Sumber gambar : Soal UN Fisika 2008 Kode Soal P4 )

Pembahasan
a) nilai konsanta pegas

b) energi potensial pegas saat x = 0,02 meter

ELASTISITAS

ELASTISITAS

Elastis atau elastsisitas adalah kemampuan sebuah benda untuk kembali ke bentuk awalnya ketika gaya luar yang diberikan pada benda tersebut dihilangkan. Jika sebuah gaya diberikan pada sebuah benda yang elastis, maka bentuk benda tersebut berubah. Untuk pegas dan karet, yang dimaksudkan dengan perubahan bentuk adalah pertambahan panjang. Benda-benda elastis juga memiliki batas elastisitas. Ada 2 macam benda yaitu: benda elastis dan benda plastis (tak elastis).

1. Hukum Hooke
Pertambahan panjang yang timbul berbanding lurus dengan gaya tarik yang diberikan. Hal ini pertama kali diselidiki pada abad 17 oleh seorang arsitek berkebangsaan Inggris yang bernama Robert Hooke. Hooke menyelidiki hubungan antara gaya tarik yang diberikan pada sebuah pegas dengan pertambahan panjang pegas tersebut.
Hooke menemukan bahwa pertambahan panjang pegas yang timbul berbanding lurus dengan gaya yang diberikan.
F x
Lebih jauh lagi, Hooke juga menemukan bahwa pertambahan panjang pegas sangat bergantung pada karakteristik dari pegas tersebut. Pegas yang mudah teregang seperti karet gelang akan mengalami pertambahan panjang yang besar meskipun gaya yang diberikan kecil. Sebaliknya pegas yang sangat sulit teregang seperti pegas baja akan mengalami pertambahan panjang yang sedikit saja meskipun diberi gaya yang besar. Karakteristik yang dimiliki masing-masing pegas ini dinyatakan sebagai tetapan gaya dari pegas tersebut. Pegas yang mudah teregang seperti karet gelang memiliki tetapan gaya yang kecil. Sebaliknya pegas yang sulit teregang seperti pegas baja memiliki tetapan gaya yang besar. Secara umum apa yang ditemukan Hooke bisa dinyatakan sebagai berikut:

F = k. x
Keterangan:
F = gaya yang diberikan pada pegas (N)
k = tetapan gaya pegas (N/m)
x = pertambahan panjang pegas (m)

2. Energi Potensial Pegas
Besar energi potensial sebuah pegas dapat dihitung dari grafik hubungan gaya yang bekerja pada pegas dengan pertambahan panjang pegas tersebut.

Ep = ½ F . x
= ½ (k . x) . x

Keterangan:
Ep = energi potensial pegas (joule)
k = tetapan gaya pegas (N/m)
x = pertambahan panjang pegas (m)

3. Modulus Elastisitas

Yang dimaksud dengan Mosdulus Elastisitas adalah perbandingan antara tegangan dan regangan. Modulus ini dapat disebut dengan sebutan Modulus Young

Tegangan (Stress) dan Regangan

Tegangan adalah gaya per satuan luas penampang. Satuan tegangan adalah N/m^2. Regangan adalah perbandingan antara pertambahan panjang suatu batang terhadap panjang awal mulanya bila batang itu diberi gaya. 

Secara matematis dapat dituliskan:

Dari kedua persamaan di atas dan pengertian modulus elastisitas, kita dapat mencari persamaan untuk menghitung besarnya modulus elastisitas, yang tidak lain adalah:

Satuan untuk modulus elastisitas adalah N/m²


4. Rangkaian Pegas
Suatu rangakaian pegas pada dasarnya tersusun dari susunan seri dan / atau susunan paralel.

1) Susunan Seri
Saat pegas dirangkai seri, gaya tarik yang dialami tiap pegas sama besarnya dan gaya tarik ini = gaya tarik yang dialami pegas pengganti ( F1 = F2 = ....Fn). Pertambahan panjang pegas pengganti seri = total pertambahan panjang tiap – tiap pegas ( = x1 + x2 + ..... xn) maka nilai konstanta pengganti = total dari kebalikan tiap – tiap tetapan pegas ( 1/ks = 1/k1 + 1/k2 + ....1/kn ).

2) Susunan Paralel
Saat pegas dirangkai paralel, gaya tarik pada pegas pengganti F = total gaya tarik pada tiap pegas ( F = F1 + F2 + ....F ). Pertambahan panjang tiap pegas sama besarnya ( xtotal = x1 + x2 + ..... xn ) maka nilai konstanta pengganti = total dari tetapan tiap – tiap pegas (kp = k1 + k2 + .... kn).